Differenza tra T-test e ANOVA
 Share
Share
 C'è una linea sottile di demarcazione tra t-test e ANOVA, cioè quando la popolazione significa che solo due gruppi devono essere confrontati, il t-test viene utilizzato, ma quando devono essere confrontati i mezzi di più di due gruppi, ANOVA è preferito.
C'è una linea sottile di demarcazione tra t-test e ANOVA, cioè quando la popolazione significa che solo due gruppi devono essere confrontati, il t-test viene utilizzato, ma quando devono essere confrontati i mezzi di più di due gruppi, ANOVA è preferito.
T-test e analisi della varianza abbreviata come ANOVA, sono due tecniche statistiche parametriche utilizzate per testare l'ipotesi. Poiché si basano sull'ipotesi comune come la popolazione da cui viene estratto il campione dovrebbe essere normalmente distribuita, l'omogeneità della varianza, il campionamento casuale dei dati, l'indipendenza delle osservazioni, la misurazione della variabile dipendente sul rapporto o il livello dell'intervallo, le persone spesso interpretano erroneamente questi Due.
Ecco un articolo presentato per farti capire la differenza significativa tra t-test e ANOVA, dai uno sguardo.
Contenuto: T-test Vs ANOVA
Grafico comparativo
| Base per il confronto | T-test | ANOVA |
|---|---|---|
| Senso | T-test è un test di ipotesi che viene utilizzato per confrontare i mezzi di due popolazioni. | ANOVA è una tecnica statistica che viene utilizzata per confrontare i mezzi di più di due popolazioni. |
| Statistica di prova | (x ̄-μ) / (s / √n) | Tra la varianza campionaria / all'interno della varianza campionaria |
Definizione di T-test
Il t-test è descritto come il test statistico che esamina se la media della popolazione di due campioni è molto diversa l'una dall'altra, utilizzando la distribuzione t che viene utilizzata quando la deviazione standard non è nota e la dimensione del campione è piccola. È uno strumento per analizzare se i due campioni sono tratti dalla stessa popolazione.
Il test si basa sulla statistica t, che presuppone che la variabile sia distribuita normalmente (distribuzione simmetrica a campana) e che la media sia nota e che la varianza della popolazione sia calcolata dal campione.
Nel test t l'ipotesi nulla assume la forma di H0: μ (x) = μ (y) contro l'ipotesi alternativa H1: μ (x) ≠ μ (y), in cui μ (x) e μ (y) rappresentano i mezzi di popolazione. Il grado di libertà del t-test è n1 + n2 - 2
Definizione di ANOVA
L'analisi della varianza (ANOVA) è un metodo statistico, comunemente usato in tutte quelle situazioni in cui si deve effettuare un confronto tra più di due mezzi di popolazione come la resa del raccolto da più varietà di semi. È uno strumento di analisi fondamentale per il ricercatore che gli consente di condurre test simultaneamente. Quando usiamo ANOVA, si presume che il campione sia estratto dalla popolazione normalmente distribuita e la varianza della popolazione sia uguale.
In ANOVA, la quantità totale di variazione in un set di dati è suddivisa in due tipi, vale a dire l'importo assegnato al caso e l'importo assegnato a cause particolari. Il suo principio di base è quello di testare le differenze tra i mezzi di popolazione valutando la quantità di variazione all'interno delle voci di gruppo, proporzionata alla quantità di variazione tra i gruppi. All'interno del campione, la varianza è dovuta al disturbo casuale inspiegabile mentre un diverso trattamento può causare tra la varianza campionaria.
Con l'uso di questa tecnica, testiamo l'ipotesi nulla (H0) in cui tutti i mezzi di popolazione sono la stessa, o ipotesi alternativa (H1) in cui almeno una media della popolazione è diversa.
Differenze chiave tra T-test e ANOVA
Le differenze significative tra T-test e ANOVA sono discusse in dettaglio nei seguenti punti:
- Un test di ipotesi che viene utilizzato per confrontare i mezzi di due popolazioni è chiamato t-test. Una tecnica statistica che viene utilizzata per confrontare i mezzi di più di due popolazioni è nota come Analisi della varianza o ANOVA.
- Statistica di test per T-test è:
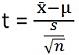 Statistica di test per ANOVA è:
Statistica di test per ANOVA è: 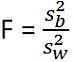
Conclusione
Dopo aver esaminato i punti precedenti, si può affermare che t-test è un tipo speciale di ANOVA che può essere utilizzato quando abbiamo solo due popolazioni per confrontare i loro mezzi. Sebbene le probabilità di errori possano aumentare se si utilizza t-test quando si devono confrontare contemporaneamente più di due medie delle popolazioni, è per questo che viene utilizzato ANOVA
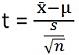 Statistica di test per ANOVA è:
Statistica di test per ANOVA è: