Differenza tra media e mediana
 Share
Share
 La tendenza centrale implica la tendenza dei punti dati a raggrupparsi attorno al suo valore centrale o medio. Le due misure di tendenza centrale più comunemente utilizzate sono media e media. Significare è definito come il valore "centrale" dell'insieme dato di dati mentre mediano è il valore "medio" nel set di dati specificato.
La tendenza centrale implica la tendenza dei punti dati a raggrupparsi attorno al suo valore centrale o medio. Le due misure di tendenza centrale più comunemente utilizzate sono media e media. Significare è definito come il valore "centrale" dell'insieme dato di dati mentre mediano è il valore "medio" nel set di dati specificato.
Una misura ideale di tendenza centrale è quella che è chiaramente definita, facilmente comprensibile, semplicemente calcolabile. Dovrebbe essere basato su tutte le osservazioni e meno influenzato dalle osservazioni estreme presenti nel set di dati.
Le persone spesso contrastano queste due misure, ma il fatto è che sono diverse. Questo articolo evidenzia in particolare le differenze di base tra media e mediana. Dare un'occhiata.
Contenuto: media Vs mediana
Grafico comparativo
| Base per il confronto | Significare | Mediano |
|---|---|---|
| Senso | Media si riferisce alla media semplice dell'insieme di valori o quantità indicato. | Mediana è definita come il numero medio in una lista di valori ordinati. |
| Che cos'è? | È una media aritmetica. | È una media posizionale. |
| rappresenta | Centro di gravità del set di dati | Centro di gravità del set di dati Punto medio del set di dati |
| applicabilità | Distribuzione normale | Distribuzione distorta |
| Valori anomali | La media è sensibile ai valori anomali. | La mediana non è sensibile ai valori anomali. |
| Calcolo | La media è calcolata sommando tutte le osservazioni e quindi dividendo il valore ottenuto con il numero di osservazioni. | Per calcolare la mediana, il set di dati è disposto in ordine ascendente o discendente, quindi il valore che cade nel centro esatto del nuovo set di dati, è mediano. |
Definizione di media
La media è la misura ampiamente utilizzata della tendenza centrale, definita come la media dell'insieme di valori. Rappresenta il modello e il valore più comune dell'intervallo di valori specificato. Può essere calcolato, sia in serie discrete che in serie continue.
La media è uguale alla somma di tutte le osservazioni divisa per il numero di osservazioni nel set di dati. Se il valore assunto da una variabile è uguale, anche la sua media sarà la stessa. La media può essere di due tipi, la media campionaria (x̅) e la media della popolazione (μ). Può essere calcolato con la formula data:
- Significato aritmetico:
 dove Σ = sigma lettera greca, indica 'somma di ...'
dove Σ = sigma lettera greca, indica 'somma di ...'
n = numero di valori - Per serie discrete:
 dove, f = frequenza
dove, f = frequenza - Per servizi continui:
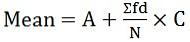 dove d = (X-A) / C
dove d = (X-A) / C
A = media presunta
C = divisore comune
Definizione di mediana
La mediana è un'altra importante misura della tendenza centrale, utilizzata per suddividere il valore in due parti uguali, vale a dire una maggiore metà del campione, una distribuzione di popolazione o di probabilità dalla metà inferiore. È il valore medio-intermedio, ottenuto quando le osservazioni sono ordinate in un ordine specifico, in ordine ascendente o discendente.
Per il calcolo della mediana, prima di tutto, organizzare le osservazioni dal più basso al più alto o dal più alto al più basso, quindi applicare la formula appropriata, secondo le condizioni riportate di seguito:
- Se il numero di osservazioni è dispari:
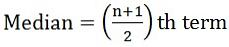 dove n = numero di osservazioni
dove n = numero di osservazioni - Se il numero di osservazioni è anche:
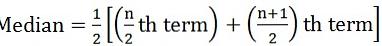
- Per serie continue:
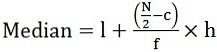 dove, l = limite inferiore della classe mediana
dove, l = limite inferiore della classe mediana
c = frequenza cumulativa della precedente classe mediana
f = frequenza della classe mediana
h = larghezza della classe
Differenze chiave tra media e mediana
Le differenze significative tra media e mediana sono fornite nell'articolo qui sotto:
- In statistica, una media è definita come la media semplice dell'insieme di valori o quantità dato. Si dice che la mediana sia il numero medio in una lista di valori ordinati.
- Mentre media è la media aritmetica, la mediana è media posizionale, in sostanza, la posizione del set di dati determina il valore della mediana.
- La media indica il centro di gravità del set di dati mentre la mediana evidenzia il valore medio del set di dati.
- La media è appropriata per i dati normalmente distribuiti. Dall'altro lato, la mediana è migliore quando la distribuzione dei dati è distorta.
- La media è fortemente influenzata dal valore estremo che non è nel caso di una mediana.
- La media viene calcolata sommando tutte le osservazioni e quindi dividendo il valore ottenuto con il numero di osservazioni; il risultato è medio A differenza della mediana, il set di dati è disposto in ordine ascendente o discendente, quindi il valore che cade nel centro esatto del nuovo set di dati è mediano.
Esempio
Trova la media e la mediana del set di dati indicato:
58, 26, 65, 34, 78, 44, 96
Soluzione: per calcolare media, è necessario dividere la somma delle osservazioni con il numero di osservazioni,

 Media = 57,28
Media = 57,28
Per calcolare la mediana, prima di tutto, disponi le serie in una sequenza, vale a dire dal più basso al più alto,
26, 34, 44, 58, 65, 78, 96
 dove n = numero di osservazioni
dove n = numero di osservazioni
Conclusione
Dopo aver esaminato i punti precedenti, possiamo dire che questi due concetti matematici sono diversi. La media aritmetica o media è considerata la migliore misura della tendenza centrale in quanto contiene tutte le caratteristiche di una misura ideale, ma ha uno svantaggio che le fluttuazioni del campionamento influenzano la media.
Allo stesso modo, la mediana è anche definita in modo univoco e facile da capire e calcolare, e la cosa migliore di questa misura è che non è influenzata dalle fluttuazioni del campionamento, ma l'unico svantaggio della mediana è che non si basa su tutti osservazioni. Per la classificazione open end, la mediana è normalmente preferita rispetto alla media.
 dove Σ = sigma lettera greca, indica 'somma di ...'
dove Σ = sigma lettera greca, indica 'somma di ...' dove, f = frequenza
dove, f = frequenza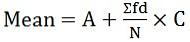 dove d = (X-A) / C
dove d = (X-A) / C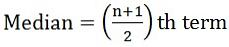 dove n = numero di osservazioni
dove n = numero di osservazioni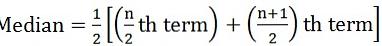
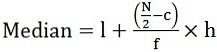 dove, l = limite inferiore della classe mediana
dove, l = limite inferiore della classe mediana Mediana = 4esimo termine = 58
Mediana = 4esimo termine = 58