Come calcolare Half Life
 Share
Share
In questa sezione impareremo l'emivita e ricaveremo la formula per calcolare l'emivita. Nella radioattività, metà vita è il tempo impiegato dalla metà dei nuclei radioattivi in un campione di un isotopo radioattivo a decadere. Il numero di nuclei radioattivi in un campione decadono in modo esponenziale nel tempo. Per calcolare l'emivita, quindi, viene utilizzata la matematica del decadimento esponenziale. L'emivita è un concetto estremamente importante per le applicazioni della radioattività. I radioisotopi introdotti negli organi di radioterapia, ad esempio, non devono rimanere nel corpo di un paziente troppo a lungo. D'altra parte, gli isotopi usati per datare artefatti storici devono avere lunghe mezze vite in modo tale che ne siano rimasti fino a oggi sufficienti per determinare l'età degli oggetti.
Differenza tra natura casuale e spontanea del decadimento radioattivo
Il decadimento radioattivo è classificato come entrambi casuale e spontaneo.
- Il decadimento radioattivo è casuale perché non siamo in grado di determinare quando un dato nucleo decadrà, o di determinare quanto tempo ci vorrà prima che un dato nucleo decada. Di conseguenza, ogni nucleo radioattivo in un campione ha la stessa probabilità di decadimento in un dato momento.
- Il decadimento radioattivo è spontaneo perché non è influenzato da condizioni esterne.
Cos'è Half Life
Il numero di nuclei radioattivi in un campione sta diminuendo, perché una volta che il nucleo decade con il decadimento alfa, beta e gamma, non possono più subire lo stesso processo di decadimento. Il numero di nuclei radioattivi nel campione diminuisce in maniera esponenziale.
Il attività, o il decadimento,è il tasso di variazione del numero di nuclei radioattivi. Questo è dato da,

Il segno negativo indica che il numero di nuclei radioattivi in un campione è decrescente col tempo. $ latex \ lambda & s = 1 $ è chiamato il decadimento costante. Dà la probabilità che un dato nucleo decada per unità di tempo. La costante di decadimento ha un valore specifico per ogni dato processo di decadimento nucleare. Più alto è il  , maggiore è la probabilità di decadimento e il numero di nuclei radioattivi nel campione diminuisce più rapidamente.
, maggiore è la probabilità di decadimento e il numero di nuclei radioattivi nel campione diminuisce più rapidamente.
Se il numero di nuclei radioattivi in un campione alla volta  è
è  , quindi il numero di nuclei radioattivi
, quindi il numero di nuclei radioattivi  nel campione dopo un po '
nel campione dopo un po '  è dato da:
è dato da:

Il numero di nuclei radioattivi nel campione diminuisce in modo esponenziale. Metà vita ( ) È la quantità di tempo impiegata per il numero di nuclei radioattivi nel tempo necessario a dimezzarsi. Se disegniamo un grafico di come il numero di nuclei radioattivi nel campione varia nel tempo, otteniamo il seguente grafico:
) È la quantità di tempo impiegata per il numero di nuclei radioattivi nel tempo necessario a dimezzarsi. Se disegniamo un grafico di come il numero di nuclei radioattivi nel campione varia nel tempo, otteniamo il seguente grafico:

Come calcolare Half Life - Curve di decadimento radioattivo
Come calcolare l'attività
L'attività del campione è proporzionale al numero di nuclei radioattivi presenti. Quindi, possiamo fare una dichiarazione equivalente,

dove  è l'attività del campione alla volta
è l'attività del campione alla volta  , con
, con  l'attività quando
l'attività quando  .
.
Se viene tracciato un grafico di attività rispetto a tempo, produrrà un grafico con la stessa forma (ad esempio, l'attività decade in modo esponenziale).
L'attività viene misurata con l'unità SI becquerel (Bq). Un'attività di 1 Bq corrisponde a un tasso di 1 decadimento al secondo. Il curie (Ci) è un'altra unità utilizzata per misurare l'attività. 1 Ci = 3,7 × 1010 bq.
Half Life Formula
Ora ricaveremo una formula per ottenere l'emivita dalla costante di decadimento. Iniziamo con,

Dopo del tempo  , il numero di metà dei nuclei radioattivi. Così,
, il numero di metà dei nuclei radioattivi. Così,  , o
, o

Prendendo il logaritmo naturale di entrambe le parti, otteniamo:

e così,

Come calcolare Half Life
Esempio 1
L'indio-112 ha un'emivita di 14,4 minuti. Un campione contiene 1,32 × 1024 atomi di Indium-112.
a) Trova la costante di decadimento
b) Scopri quanti atomi di Indium-112 saranno lasciati nel campione dopo 1 ora.
a) Da  ,
,

b) Uso  ,
,  atomi.
atomi.
Esempio 2
Durante un trattamento per il cancro della tiroide, ad un paziente viene dato un campione di Iodio-131 da ingerire, che ha un'attività di 1,10 MBq. L'emivita di iodio 131 è di 8,02 giorni. Trova l'attività di iodio-131 nel corpo del paziente dopo 5 giorni di ingestione.
Noi usiamo  . Innanzitutto, lavoriamo
. Innanzitutto, lavoriamo  :
:

Poi,
 MBq.
MBq.
Nota:
- Abbiamo calcolato direttamente la costante di decadimento al giorno e mantenuto l'emivita anche in giorni. Quindi i giorni cancellati quando abbiamo calcolato
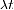 e non c'era bisogno di convertire i tempi in secondi (che avrebbe funzionato bene, ma avrebbe comportato un po 'più di calcolo)
e non c'era bisogno di convertire i tempi in secondi (che avrebbe funzionato bene, ma avrebbe comportato un po 'più di calcolo) - In realtà, l'attività sarebbe più piccola. Questo perché c'è anche un'emivita biologica associata all'attività. Questa è la velocità con cui il paziente espelle i nuclei radioattivi dal loro corpo.
Esempio 3
Calcola l'emivita di un isotopo radioattivo la cui attività si riduce del 4% in 1000 anni.
4% = 0,04. Ora abbiamo
 . Prendendo ln di entrambe le parti,
. Prendendo ln di entrambe le parti,
 per anno.
per anno.
 216 anni.
216 anni.
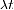 e non c'era bisogno di convertire i tempi in secondi (che avrebbe funzionato bene, ma avrebbe comportato un po 'più di calcolo)
e non c'era bisogno di convertire i tempi in secondi (che avrebbe funzionato bene, ma avrebbe comportato un po 'più di calcolo)