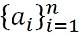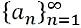Differenza tra sequenza e serie

In matematica e statistica, la linea che delimita sequenza e serie è sottile e sfocata, a causa della quale molti pensano che questi termini siano la stessa cosa. Tuttavia, la nozione di sequenza differisce dalle serie nel senso che sequenza si riferisce ad una disposizione nell'ordine particolare in cui i termini correlati si susseguono, cioè ha una prima unità identificata, una seconda unità, una terza unità e così via..

Quando una sequenza segue una particolare regola, viene chiamata progressione. Non è esattamente lo stesso di serie che è definito come la sommatoria degli elementi di una sequenza. Prendi una lettura dell'articolo per conoscere la differenza significativa tra sequenza e serie.

Contenuto: Sequence Vs Series

Grafico comparativo

Base per il confronto	Sequenza	Serie
Senso	La sequenza è descritta come l'insieme di numeri o oggetti che segue un determinato modello.	La serie si riferisce alla somma degli elementi della sequenza.
Ordine	Importante	A volte importante
Esempio	1, 3, 5, 7, 9, 11 ... n ...	1 + 3 + 5 + 9 + 11 ... n ...

Definizione di Sequenza

In matematica, un insieme ordinato di oggetti o numeri, come a₁, un₂, un₃, un₄, un₅, un₆... a_{n ... .}si dice che sia in una sequenza, se, come per certe regole, ha un valore definito. I membri della sequenza sono chiamati termine o elemento che è uguale a qualsiasi valore del numero naturale. Ogni termine in una sequenza è correlato al termine precedente e successivo. In generale, le sequenze hanno regole o pattern nascosti, che ti aiutano a scoprire il valore del prossimo termine.

L'ennesimo termine è la funzione del numero intero n (positivo), considerato come il termine generale della sequenza. Una sequenza può essere finita o infinita.

Sequenza finita: Una sequenza finita è quella che si ferma alla fine dell'elenco di numeri a₁, un₂, un₃, un₄, un₅, un₆... a_n, è rappresentato da:
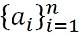
Sequenza infinita: Una sequenza infinita si riferisce a una sequenza che è senza fine, a₁, un₂, un₃, un₄, un₅, un₆... a_{n ... .}., è rappresentato da:

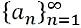
Definizione di serie

L'aggiunta dei termini di una sequenza (a_n), è noto come serie. Come la sequenza, anche le serie possono essere finite o infinite, dove una serie finita è una serie che ha un numero finito di termini scritti come₁+ un₂+ un₃ + un₄+ un₅ + un_{6 +}... a_n. A differenza delle serie infinite, in cui il numero di elementi non è finito o è infinito, scritto come a₁+ un₂+ un₃ + un₄+ un₅ + un_{6 +}... a_n+_{... .}

Se una₁+ un₂+ un₃ + un₄+ un₅ + un_{6 +}... a_n = S_n, allora S_n è considerato come la somma di n elementi della serie. La somma dei termini è spesso rappresentata dalla lettera greca sigma (Σ). Quindi,

Differenze chiave tra sequenza e serie

La differenza tra sequenza e serie può essere tracciata chiaramente per i seguenti motivi:

La sequenza è definita come la raccolta di numeri o oggetti che seguono uno schema definito. Quando gli elementi della sequenza vengono sommati, sono noti come serie.
L'ordine è importante in una sequenza, poiché esiste una determinata regola che prescrive lo schema della sequenza. Quindi, 1, 2, 3 ° è diverso da 3, 1, 2. D'altra parte, in un ordine di serie di apparizioni può o non può importare, come nel caso di serie assolutamente convergenti l'ordine non ha importanza. Quindi, 1 + 2 + 3 è uguale a 3 + 1 + 2, solo la loro sequenza è diversa.

Conclusione

Anche la progressione aritmetica (A.P.) e la progressione geometrica (G.P.) sono sequenze, non serie. La progressione aritmetica è una sequenza in cui esiste una differenza comune tra i termini consecutivi come 2, 4, 6, 8 e così via. Al contrario, in una progressione geometrica, ogni elemento della sequenza è il multiplo comune del termine precedente, come 3, 9, 27, 81 e così via. Allo stesso modo, Sequenza di Fibonacci è anche una delle sequenze infinite popolari, in cui ogni termine è ottenuto sommando i due precedenti termini 1, 1, 3, 5, 8, 13, 21 e così via.

Formazione scolastica