Come trovare gli asintoti di un'iperbole
 Share
Share
Iperbole
L'iperbole è una sezione conica. Il termine iperbole si riferisce alle due curve disconnesse mostrate nella figura.
Se gli assi principali coincidono con gli assi cartesiani, l'equazione generale dell'iperbole ha la forma:

Queste iperboli sono simmetriche attorno all'asse y e sono conosciute come iperbole dell'asse y. L'iperbole simmetrica attorno all'asse x (o l'iperbole dell'asse x) è data dall'equazione,
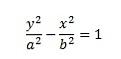 Come trovare gli asintoti di un'iperbole
Come trovare gli asintoti di un'iperbole
Per trovare gli asintoti di un'iperbole, usa una semplice manipolazione dell'equazione della parabola.
io. Per prima cosa porta l'equazione della parabola alla forma sopra indicata
Se la parabola è data come mx2+NY2=l, definendo
un= √ (l/m) e B= √ (-l/n) dove l<0
(Questo passaggio non è necessario se l'equazione è data in standard da.

ii. Quindi, sostituire il lato destro dell'equazione con zero.

iii. Factorize l'equazione e prendere soluzioni

Pertanto, le soluzioni sono ,

Le equazioni degli asintoti sono

Le equazioni degli asintoti per l'iperbole dell'asse x possono anche essere ottenute con la stessa procedura.
Trova gli asintoti di un'iperbole - Esempio 1
Considera l'iperbole data dall'equazione x2/ 4-y2/ 9 = 1. Trova le equazioni degli asintoti.

Riscrivi l'equazione e segui la procedura sopra.
X2/ 4-y2/ 9 = x2/ 22 -y2/ 32 = 1
Sostituendo il lato destro con zero, l'equazione diventa x2/ 22 -y2/ 32 = 0.
Dare un valore e prendere soluzione all'equazione,
(X / 2-y / 3) (x / 2 + y / 3) = 0
Le equazioni degli asintoti sono,
3x-2y = 0 e 3x + 2y = 0
Trova gli asintoti di un'iperbole - Esempio 2
- L'equazione di una parabola è data come -4x² + y² = 4

Questa iperbole è un'iperbole dell'asse x.
Riorganizzare i termini dell'iperbole nello standard da dà
-4x2+ y2= 4 => y2/ 22 -X2/ 12 = 1
Factorizing l'equazione fornisce quanto segue
(Y / 2-x) (y / 2 + x) = 0
Pertanto, le soluzioni sono y-2x = 0 ey + 2x = 0.
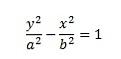 Come trovare gli asintoti di un'iperbole
Come trovare gli asintoti di un'iperbole 