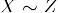Differenza tra uguale ed equivalente
 Share
Share
Differenza principale - Uguale vs Equivalente
Pari e equivalente sono termini usati frequentemente in matematica. Il differenza principale tra uguale ed equivalente è quel termine uguale si riferisce a cose che sono simili in tutti gli aspetti, mentre il termine equivalente si riferisce a cose che sono simili in un aspetto particolare. Si noti che nel insiemistica, le parole "uguale" e "equivalente" hanno significati specifici, come vedremo in seguito.
Cosa significa uguale
In generale, due cose sono uguali se sono simili sotto tutti gli aspetti.
Nel caso della teoria degli insiemi, due insiemi sono uguali se entrambi contengono gli stessi elementi. Il ordine in cui sono elencati in un set non importa. Ad esempio, supponiamo
 e
e
 poi,
poi,
il set  è uguale al set
è uguale al set  .
.
Cosa significa Equivalente
Si possono dire due cose equivalenti se sono simili sotto una particolare condizione. Pertanto, se due entità sono equivalente in gran parte dipende a condizione che usiamo per descrivere la loro equivalenza. Ad esempio, i numeri 2 e 7 sono equivalenti nel senso che sono entrambi numeri primi. Tuttavia, se la condizione che ci interessa è scoprire se i numeri sono pari, allora in questo senso 2 e 7 lo sono non equivalente. Usiamo i simboli  o
o  per indicarlo
per indicarlo  e
e  sono equivalenti.
sono equivalenti.
Una volta definito un criterio, le cose che equivalgono soddisfano il relazioni di equivalenza:
- La riflessività:
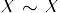
- Simmetria: Se
 , poi
, poi 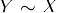
- transitività: Se
 e
e 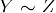 , poi
, poi 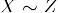
Nella teoria degli insiemi, ci sono due serie equivalente se hanno lo stesso numero di elementi. Gli stessi elementi non devono necessariamente essere uguali, solo il numero di elementi deve essere lo stesso. Ad esempio, supponiamo
 e
e
 poi,
poi,
i set  e
e  sono equivalenti.
sono equivalenti.

Simboli per esprimere l'uguaglianza e l'equivalenza
Differenza tra uguale ed equivalente
Significato generale
Quando sono due cose pari, sono simili in tutti gli aspetti.
Quando le cose sono equivalente, sono simili in un aspetto particolare.
In Set Theory
Quando ci sono due serie pari, contengono gli stessi elementi.
Quando ci sono due serie equivalente, contengono lo stesso numero di elementi.
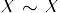
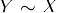
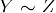 , poi
, poi