Differenza tra le trasformate di Laplace e di Fourier
 Share
Share
Trasformazioni di Laplace vs Fourier
Sia la trasformata di Laplace che la trasformata di Fourier sono trasformazioni integrali, che sono comunemente utilizzate come metodi matematici per la risoluzione di sistemi fisici matematicamente modellati. Il processo è semplice Un modello matematico complesso viene convertito in un modello più semplice e risolvibile utilizzando una trasformazione integrale. Una volta risolto il modello più semplice, viene applicata la trasformazione integrale inversa, che fornirebbe la soluzione al modello originale.
Ad esempio, poiché la maggior parte dei sistemi fisici risulta in equazioni differenziali, possono essere convertiti in equazioni algebriche o in equazioni differenziali facilmente risolvibili con una trasformata integrale. Quindi risolvere il problema diventerà più facile.
Qual è la trasformata di Laplace?
Data una funzione f (t) di una variabile reale t, la sua trasformata di Laplace è definita dall'integrale 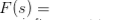 (ogni volta che esiste), che è una funzione di una variabile complessa S. Solitamente è denotato da L f (t). La trasformata inversa di Laplace di una funzione F(S) è considerata la funzione f (t) in modo tale che L f (t) = F(S), e nella solita notazione matematica scriviamo, L -1F(S) = f (t).La trasformazione inversa può essere resa univoca se non sono consentite funzioni null. Si possono identificare questi due come operatori lineari definiti nello spazio delle funzioni, ed è anche facile vedere che, L -1L f (t) = f (t), se non sono consentite funzioni nulle.
(ogni volta che esiste), che è una funzione di una variabile complessa S. Solitamente è denotato da L f (t). La trasformata inversa di Laplace di una funzione F(S) è considerata la funzione f (t) in modo tale che L f (t) = F(S), e nella solita notazione matematica scriviamo, L -1F(S) = f (t).La trasformazione inversa può essere resa univoca se non sono consentite funzioni null. Si possono identificare questi due come operatori lineari definiti nello spazio delle funzioni, ed è anche facile vedere che, L -1L f (t) = f (t), se non sono consentite funzioni nulle.
La seguente tabella elenca le trasformate di Laplace di alcune delle funzioni più comuni.

Qual è la trasformata di Fourier?
Data una funzione f (t) di una variabile reale t, la sua trasformata di Laplace è definita dall'integrale 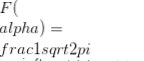 (ogni volta che esiste), ed è solitamente indicato da F f (t). La trasformazione inversa F -1F(α) è dato dall'integrale
(ogni volta che esiste), ed è solitamente indicato da F f (t). La trasformazione inversa F -1F(α) è dato dall'integrale  . La trasformata di Fourier è anche lineare e può essere pensata come un operatore definito nello spazio delle funzioni.
. La trasformata di Fourier è anche lineare e può essere pensata come un operatore definito nello spazio delle funzioni.
Usando la trasformata di Fourier, la funzione originale può essere scritta come segue purché la funzione abbia solo un numero finito di discontinuità ed è assolutamente integrabile. 
Qual è la differenza tra le trasformate di Laplace e di Fourier?
- Trasformata di Fourier di una funzione f (t) è definito come
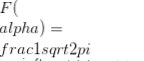 , mentre la trasformata di laplace è definita essere
, mentre la trasformata di laplace è definita essere 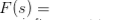 .
. - La trasformazione di Fourier è definita solo per le funzioni definite per tutti i numeri reali, mentre la trasformazione di Laplace non richiede la definizione della funzione per impostare i numeri reali negativi.
- La trasformata di Fourier è un caso speciale della trasformata di Laplace. Si può vedere che entrambi coincidono per numeri reali non negativi. (Prendiamo S nel Laplace essere iα + β dove α e β sono reali tali e β= 1/√ (2ᴫ))
- Ogni funzione che ha una trasformata di Fourier avrà una trasformata di Laplace ma non viceversa.
