Differenza tra distribuzione binomiale e normale

Distribuzione binomiale vs normale
 

Le distribuzioni di probabilità di variabili casuali giocano un ruolo importante nel campo delle statistiche. Di quelle distribuzioni di probabilità, la distribuzione binomiale e la distribuzione normale sono due delle più comuni nella vita reale.

Cos'è la distribuzione binomiale?

La distribuzione binomiale è la distribuzione di probabilità corrispondente alla variabile casuale X, che è il numero di successi di a sequenza finita di esperimenti indipendenti si / no ognuno dei quali ha una probabilità di successo p. Dalla definizione di X, è evidente che è una variabile casuale discreta; pertanto, anche la distribuzione binomiale è discreta.

La distribuzione è indicata come X ~B(n,p) dove n è il numero di esperimenti e p è la probabilità di successo. Secondo la teoria della probabilità, possiamo dedurlo B(n,p) segue la funzione di massa di probabilità . Da questa equazione, si può dedurre ulteriormente che il valore atteso di X, E (X) = np e la varianza di X, V (X) = np(1-p).

Ad esempio, considera un esperimento casuale di lancio di una moneta 3 volte. Definisci il successo come ottenere H, il fallimento come ottenere T e la variabile casuale X come il numero di successi nell'esperimento. Poi X~B(3, 0.5) e la funzione di massa di probabilità di X dato da . Pertanto, la probabilità di ottenere almeno 2 H è P (X ≥ 2) = P (X = 2 o X = 3) = P (X = 2) + P (X = 3) = ³C₂(0.5²) (0.5¹) + ³C₃(0.5³) (0.5⁰) = 0,375 + 0,125 = 0,5.

Cos'è la distribuzione normale?

La distribuzione normale è la distribuzione di probabilità continua definita dalla funzione di densità di probabilità, . I parametri denota la media e la deviazione standard della popolazione di interesse. quando la distribuzione è chiamata distribuzione normale standard.

Questa distribuzione è chiamata normale poiché la maggior parte dei fenomeni naturali seguono la distribuzione normale. Ad esempio, il QI della popolazione umana è normalmente distribuito. Come si vede dal grafico, è unimodale, simmetrico rispetto alla media e alla campana. La media, la modalità e la mediana sono coincidenti. L'area sotto la curva corrisponde alla porzione della popolazione, soddisfacendo una determinata condizione.

Le porzioni di popolazione nell'intervallo , , sono rispettivamente del 68,2%, 95,6% e 99,8%.

Qual è la differenza tra distribuzioni binomiali e normali?

• La distribuzione binomiale è una distribuzione di probabilità discreta mentre la distribuzione normale è una distribuzione continua.
• La funzione di massa di probabilità della distribuzione binomiale è , mentre la funzione di densità di probabilità della distribuzione normale è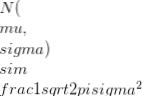
• La distribuzione binomiale è approssimata alla distribuzione normale in determinate condizioni, ma non viceversa.